Radical aritmético e suas propriedades!

A radiciação é a operação inversa da potenciação. É muito utilizada na obtenção de solução de equações e na simplificação de expressões aritméticas e algébricas. Vamos definir essa operação e analisar suas propriedades.
Dados um número real não negativo x e um número natural n ≥ 1, chama-se raiz enésima de x o número real não negativo y tal que yⁿ = x. O símbolo utilizado para representar a raiz enésima de x é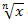  e é chamado de radical. Nesse símbolo, x é o radicando e n é o índice.

Pela definição de radiciação, temos que:

Exemplo 1.

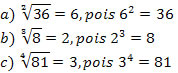
Propriedades da radiciação.

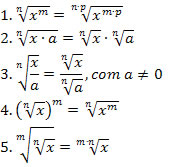
Exemplo 2. Simplifique a expressão

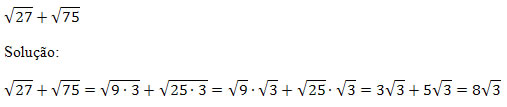
Exemplo 3. Racionalize as seguintes frações:
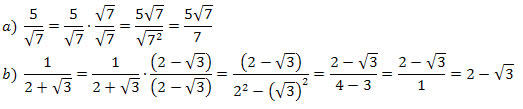
Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número.

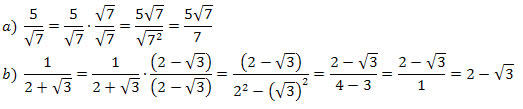
Exemplo 4. Verifique as propriedades da radiciação.

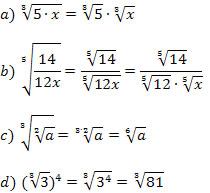
Exemplo 5. Obtenha a forma mais reduzida possível da expressão:

Solução: Podemos reescrever cada uma das raízes utilizando as propriedades da radiciação.

Postado por: Beatriz, Paula e Irivaneide.